Karar Mantık Yapısı İle Problem Çözme

Mehmet ÇOLAK 27 Kasım 201724 Aralık 2017 0 Comments çözme, karar mantık yapısı, problem

1. Karar Mantık Yapısı

Karar yapıları, bilgisayara iki ya da daha fazla seçenek arasından seçim yapmak hakkı tanıyan önemli ve güçlü bir mantık yapısıdır. Eğer karar yapıları olmasaydı bilgisayarlar hızlı bir hesap makinesi olmanın ötesine gidemezdi. Karar yapıları, insanın düşünme tarzına çok uygun olduğu için anlaşılması son derece kolaydır. Karmaşık durumlarda karar vermek zorlaştığı için programcının kararların arkasında yatan nedenleri çok iyi anlayarak tasarım yapması gerekir. Ayrıca bir karar durumunun çok farklı şekillerde ifade edilebilmesi de bu karmaşıklığa neden olabilmektedir.

Karar mantık yapısı, if-then-else (eğer-koşul sağlanırsa-x, değilse y) yönergesini kullanır. Bu durumda, eğer bir koşul doğru ise belli yönergeler; değilse farklı yönergeler çalıştırılabilir. “else” kısmı kullanılmak zorunda değildir; bazen bu durumlarda hiçbir yönerge olmayabilir. Aşağıdaki yapıyı ve satır başlarındaki boşlukları inceleyelim.

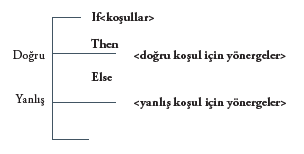
Bu kodlamada yer alan koşul;

Mantıksal bir ifade (AND (VE), OR (YA DA) veya NOT (DEĞİL))

İlişkisel operatörleri kullanan bir ifade (<, >, <=, >=, =),

Sonucu doğru ya da yanlış çıkan mantıksal bir değişken,

Bu üç seçeneğin birleşiminden oluşan bir ifade olabilir.

Koşullara ilişkin açıklamalar aşağıdaki gibi olabilir:

A < B (A ve B sayısal, karakter ya da dizi gibi aynı veri türündedir.)

X + 5 > = Z ( X ve Z sayısal veridir.)

E < 5 OR F > 12 ( E ve F sayısal veridir.)

(A < B) AND (X = 10 OR Y >15) (A ve B sayısal, karakter ya da dizi gibi aynı veri türündedir ve X ve Y sayısal veridir.)

Mantıksal operatörler bir ya da daha fazla durumu bağlamak için kullanılır. Örneğin sürücü belgesi alabilmek için 18 yaşını doldurmuş ve bir sürücü kursunu başarı ile tamamlamış olma şartı vardır. Bu örnekteki kontrol, bu iki durumu AND operatörü ile bağlayarak kontrol etmeyi gerektirir.

1.1. Tek Koşullu Yapılar

Tek bir koşulun sorgulandığı döngü yapısı için akış şeması aşağıdaki gibidir:

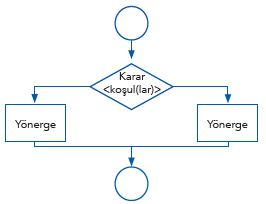
Koşulun sağlanıp sağlanmaması durumuna göre programın akışı değişir ve program, karara uygun yönergelerle çalışmaya devam eder. Hiçbir zaman üçüncü bir seçenek olamaz çünkü karar sembolünden yalnızca iki olasılık çıkabilir. Diğer bir ifade ile belirtilen durum ya doğrudur ya da yanlıştır. Örneğin bir öğrencinin puan ortalamasına bakarak Geçme/Kalma durumunu belirleyen bir program yazalım.

Bu programın algoritması aşağıdaki gibi olacaktır:

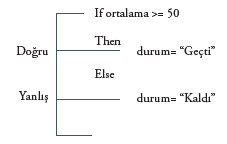
Bu programa ait akış şeması ise şu şekildedir:

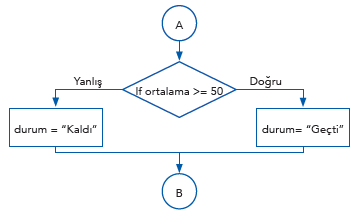
Birden fazla koşulun olduğu durumlar biraz daha karmaşıktır. Bu tür kararlarda durumları birleştirmek için mantık operatörlerinden yararlanılır. Durumlar arttıkça karar yapısı da karmaşık hâle gelir ve “Doğru” ya da “Yanlış” için atılacak adım sayısı da artar.

1.2. Çok Koşullu Karar Yapıları

Birden fazla karar içeren algoritmaları yazmak için kullanılacak üç tür karar yapısı vardır: Düz mantık, Pozitif Mantık ve Negatif Mantık. Düz mantık bütün koşulların doğrusal olarak işlenmesi anlamına gelir. Bu durumda else ile ifade edilen diğer seçeneği bulunmaz. Koşul yanlış olduğunda program doğrudan bir sonraki koşula geçer, koşul doğru ise gerekli işlemler yapıldıktan sonra bir sonraki koşula geçilir. Program akışında bütün koşullar sıra ile gözden geçirilir. Diğer yandan, pozitif mantık ile bütün yönergeler işlenmez. Eğer koşul doğru ise bu kararların yönergeleri yerine program akışı modül içinde devam eder. Koşul doğru olduğu sürece akış bu şekildedir ancak koşulun yanlış olma durumunda diğer koşula geçilir ve doğru olana kadar devam edilir. Negatif mantık da pozitif mantığa benzemekle beraber burada program akışı karar yanlış olduğu sürece devam eder. Bazı karar durumları bu türlerin bir ya da birkaçını kullanmayı gerektirebilir.

1.3. İç İçe Karar Yapıları

Çoklu karar yapıları içeren algoritmalarda eğer koşullarını iç içe yazmamız gerekebilir. Bu durumda pozitif ve negatif mantık yapıları kullanılabilir; düz mantık yapısı kullanılmaz. Aşağıdaki algoritma, öğrencinin puan ortalamasına göre Geçme/Kalma durumunu kontrol ettikten sonra, geçiyorsa öğrencinin belge alma durumunu belirlemektedir. Bu durumda bu örneğin algoritmasını aşağıdaki biçimde düzenleyebiliriz.

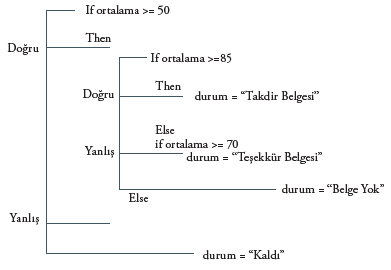
Akış şeması ise şu şekilde olacaktır:

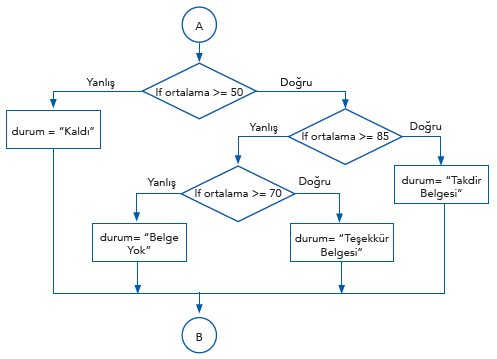
2. Düz Mantık Kullanımı

Düz mantık ile çalışan kararlarda bütün koşullar test edilir. Bir koşulun test edilmesi, “Doğru” ya da “Yanlış” sonuç elde etmek için durumun işlenmesidir. Düz mantık çözümlerin içinde en yetersizi, çözüm olarak nitelendirilebilir çünkü bütün koşulların test edilmesi, programın çalışmasını da uzatır. Bazen birbiri ile ilişkisiz durumlar olduğunda ya da tüm durumların kontrolü gerektiğinde bunu kullanmak mecburi olmaktadır. Düz mantık yapısı, genellikle diğer karar yapıları ile bir arada kullanılır.

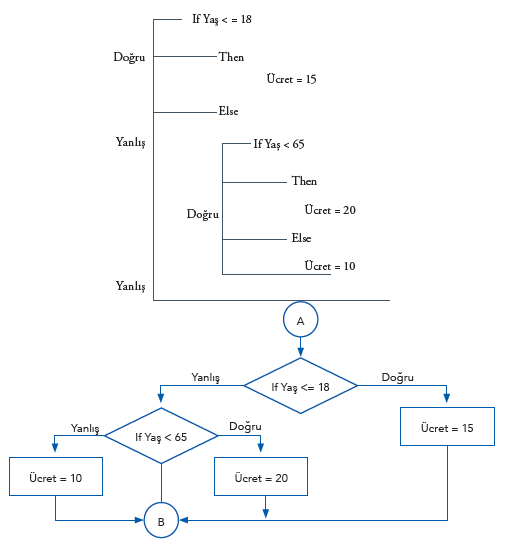
Şimdi düz mantık ile çözülebilen bir örneği inceleyelim. Tiyatro bileti alırken bilet fiyatı yaşa göre değişmektedir. Yaşı 18’den küçük olanlar için bilet ücreti 15 TL; yaşı 18’den büyük ve 65’ten küçük olanlar için 20 TL ve yaşı 65’ten büyük olanlar için 10 TL olarak belirlenmiştir. Bu durumda tiyatro seyircilerinin yaşlarına göre bilet almalarına olanak sağlayan bir çözüm geliştirmemiz gerekir.

Bu problemin çözümü için algoritma şu şekildedir:

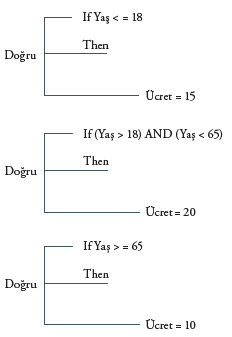
Bu problemin akış şeması ise aşağıdaki gibidir.

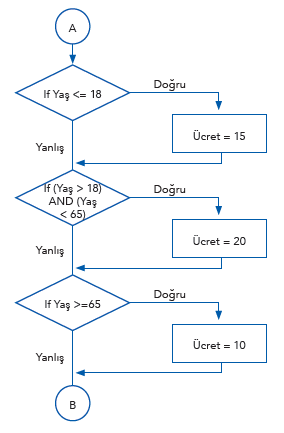
Algoritma ve akış şeması içerisinde “else” kullanılmadığına dikkat ediniz. Kontrol edilen koşul yanlış ise doğrudan bir sonraki koşul kontrol edilmektedir ki bu yüzden “değilse” durumuna gerek yoktur. Kontrol edilen durum doğru olsa ve işlem yapılsa bile bütün koşullar yine de sıra ile kontrol edilmektedir. Program çoğu durumda gereksiz kontroller yapmaktadır.

3. Pozitif Mantık Kullanımı

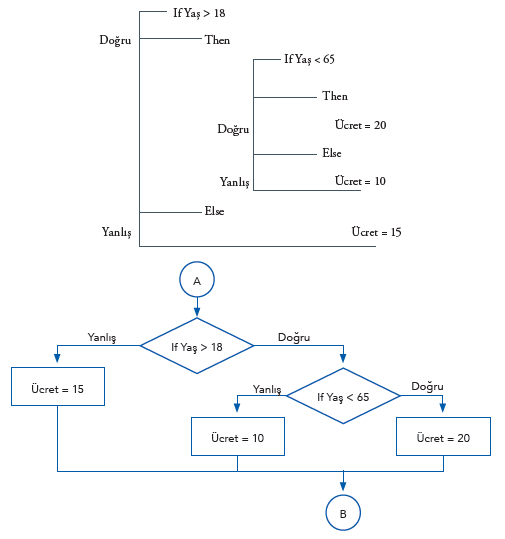
Düşünme biçimimize en çok benzeyen yapı olması nedeni ile pozitif mantık kullanımı en kolay yapıdır. Pozitif mantık her zaman iç içe If/Then/Else yapısını kullanır. Bu yapı; kullanıldığında genellikle bilgisayardan, koşulun doğru olması durumunda işlem yapması, yanlış olması durumunda farklı bir karar vermesi beklenir. Böylece daha az adımda karar verilebilir. Bir önceki problemin bu yaklaşım ile çözüm algoritmasını ve akış şemasını inceleyelim.

4. Negatif Mantık Kullanımı

Genellikle tersten düşünmediğimiz için negatif mantık yapısı, kurgusu, programcılara en zor gelen yapıdır. Negatif mantık kullanıldığında bilgisayardan, koşulun doğru olması durumunda farklı yönergeleri takip etmesi beklenir. Negatif mantık kullanmak, kontrol edilecek koşul sayısını azalttığından programı daha anlaşılır kılarak geliştirir.

5. Mantık Dönüşümleri

Bazen programın yeterliğini ve okunabilirliğini arttırmak için karar mantık yapılarını, pozitiften negatife ya da tam tersine dönüştürmek gerekebilir. İşlenmesi gereken yönergelerin doğası ve sayısı gereği ya da işlenecek yönerge olmadığı için bazen çözümün yapısı, kullandığımız mantık yapısına uymaz.

Karar verilirken koşulun yanlış olduğunda uygulanacak yönergeler olmasa bile her zaman doğru olduğu durum için uygulanacak yönergeler olmalıdır. Eğer doğru olması koşuluna uygun yönerge yoksa mantık yapısını dönüştürmek yerinde olacaktır.

Pozitif mantıktan diğerine ya da tam tersi biçimde dönüşüm yapmak için aşağıdaki kuralları uygulayınız.

Tüm < koşullarını >= ile değiştirin.

Tüm < koşullarını > ile değiştirin.

Tüm > koşullarını <= ile değiştirin.

Tüm >= koşullarını > ile değiştirin.

Tüm = koşullarını <> ile değiştirin.

Tüm <> koşullarını = ile değiştirin.

Then kapsamındaki tüm yönergeleri else kapsamı ile karşılıklı olarak değiştirin.

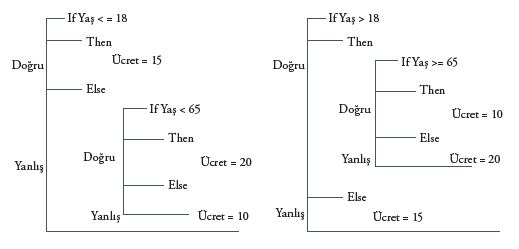
Bu dönüşüm daha önce incelediğimiz problemin çözümü için şu biçimde yapılmaktadır:

6. Hangi Mantık Yapısı?

Bir problemi çözmek için hangi karar yapısını seçeceğimize nasıl karar vereceğiz? Bunun en kolay yolu her 3 yapı için çözümü yazmak ve bu çözümler içinden en hızlı, kolay algılanan ve en az koşulla çalışanı seçmektir. Her zaman aynı yapıyı kullanmak ya da problemden istenildiği sıradaki yönergeleri kullanarak çözüm üretmek, sıkça başvurulan yollardır ancak bu yaklaşımlar her zaman en etkili çözüm ile sonuçlanmayabilir.

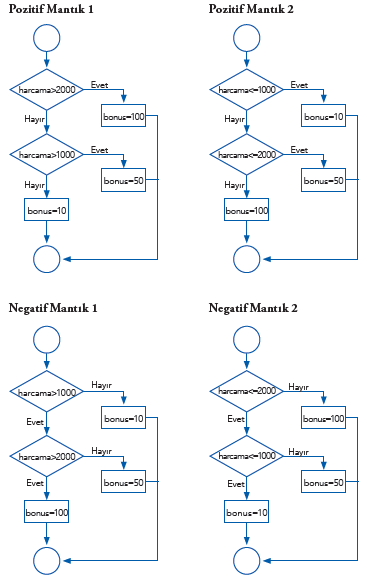
Şimdi bir problemi çözmenin 4 farklı yolunu inceleyelim. Harcanan para miktarına göre belli sayılarda “bonus” verilmesi için farklı mantık yapılarında akış şemaları şu şekildedir:

Mantık yapısına ilişkin seçim konusunda düşünürken aşağıdaki sorulara yanıt aramak önemlidir.

Hangi mantık yapısı, programı daha anlaşılır kılmaktadır?

Hangi mantık yapısını yönetmek ve değiştirmek daha kolaydır?

Veriye ilişkin fazla bilgi yokken en az sayıda koşul kontrolü yapan, hangi mantık yapısıdır?

Veri sunulduğunda en az koşul kontrolünü yapan mantık yapısı hangisidir?

7. Karar Tabloları

Birden fazla koşul ve çoklu eylem içeren bir probleminiz var. Bu durumda farklı koşullar için bütün eylemleri keşfetmek ve hatta koşul birlikteliklerine göre olası eylemleri belirlemek zor ve karmaşık bir süreç olur. Bu süreci basitleştirmenin yolu karar tablosu kullanmaktır. Karar tabloları, problemi birlikte çözdüğünüz kişi ile iletişim sağlamak ve süreci anlaşılır kılmak için çok kullanışlı bir araçtır. Karar tablosu, problem çözme mantığını tablo biçiminde gösteren bir araçtır. Akış şemalarının alternatifi de olabilir.

Bir karar tablosu 4 bölümden oluşur:

Koşullar: Tablonun sol üst bölümüne olası tüm koşullar yazılır.

Eylemler: Sol alt bölümde, şartların birleşimleri sonucu yapılan tüm olası eylemler listelenir.

“Doğru” ve “Yanlış” koşulların birleşimleri: Kurallar, sağ üst bölümde oluşturulur. Şartın durumuna bağlı olarak şartın karşılığındaki olasılıkları ifade eden gösterimler kullanılır. Örneğin Evet, Hayır’ı temsil için E ve H harf leri kullanılır.

Durumların birleşimlerine ilişkin gerçekleşecek eylemler: Sağ alt bölümde ise verilen bir kural için geçerli olan eylemlerin gösteriminde “X” simgesi kullanılır.

“Doğru” ve “Yanlış” koşulların olası bileşkelerini gösteren, her biri küçük bölmelere ayrılmış, temelde dört bölüme ayrılmış bir dikdörtgen düşünebilirsiniz. Olası bileşkelerin sayısını 2koşul sayısı şeklinde hesaplayın. Örneğin 2 koşulunuz varsa 22=4 olası bileşkeniz; 4 koşulunuz varsa 24=16 olası bileşkeniz var demektir. Bu karar tablosuna bakarak daha sonra akış şeması oluşturulabilir.

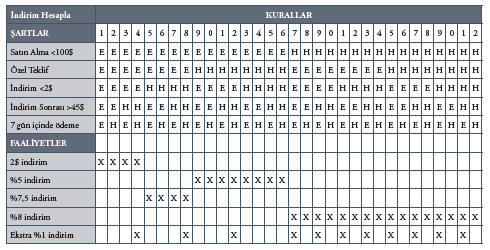
Aşağıda örnek bir karar tablosu görüyorsunuz: