Doğrusal Mantık Yapısı İle Problem Çözme

1. Doğrusal Mantık Yapısı

Problem çözme sürecinde çok basit ve çok sık kullanılan yaklaşımlardan biri doğrusal mantık yapısıdır. Bilgisayara birbiri ardına algoritmanın başından sonuna kadar sırası ile işlemesi gereken komutları veren bir programcı, bu yaklaşımı kullanıyor demektir. Algoritma ve akış şeması genel olarak şu şekildedir:

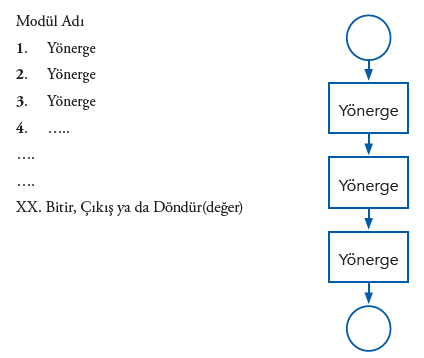
Matematiksel bir formülün hesaplanması, kullanıcının girdiği veriye dayalı basit işlemler yaparak sonucu döndürmek gibi durumlarda, doğrusal mantık yapısı kullanılır. Bir dairenin alanını hesaplama, 3 kişinin yaş ortalamasını bulma, küçük harf olarak girilen metni büyük harfe çevirme gibi işlemler buna örnek olarak verilebilir.

2. Çözüm Üretilmesi

Bir önceki bölümde çözüm üretirken kullanılacak bazı yaklaşımları incelemiştik.

Problem Analiz Çizelgesi

Etkileşim Çizelgesi

GSÇ Çizelgesi

Birleşim Çizelgesi ve Veri Sözlüğü

Algoritmalar ve Akış Şemaları

Çözümün Test Edilmesi

Bu adımları izlemenin, çözümü ne kadar kolaylaştırdığını ve özellikle karmaşık problemlerin çözümünde ne kadar önemli olduğunu unutmayalım. Şimdi bir örneği ele alalım.

Problem: Sevgi Merit, önümüzdeki 5 yıl boyunca kendisine en iyi faizi verecek bankayı aramaktadır. Sevgi, ilgili bankaya 20.000 TL değerinde yatırım yapacaktır. Faiz hesaplaması için kullanılan standart formül şu şekildedir:

Miktar = A * (1 + F/S)^(Y * S)

A = Anapara (Bu örnek için 20.000)

F = Faiz Yüzdesi (Bankanın müşteriye ödeyeceği kârın anaparaya oranı) Y = Yıl (Anaparanın değerlendirilme süresi)

S = Bileşik Faiz İçin Süre

Örneğin çözümünü aşağıdaki başlıklar altında inceleyelim:

2.1. Problem Analiz Çizelgesi

Öncelikle yapılması gereken, problem analizidir yani elde ne olduğu ve bizden ne istendiğini açık ve net biçimde analiz etmektir.

Bu çizelge hazırlandıktan sonra olası çözüm seçenekleri içerisinden en etkili ve esnek olan çözümün seçilmesi gerekir. Yukarıdaki çizelgede 1 ve 3 numaralı çözümler en uygun çözüm olarak seçilebilir. Faizi 2 numaralı seçenekte olduğu gibi sabit olarak tanımlarsak bunu, her banka için değiştirmemiz gerekir ki bu da programın esnek olmasını önler. En son seçenekteki tüm bankalar için programın çalışması ise çok fazla değişken tanımlanması gerektirdiğinden karışıklığa neden olabilir. Bu nedenle bütün verileri değişken olarak tanımlamak ve her seferinde tek bir banka için işlem yapmak, esnek ve uygun bir çözüm olarak ortaya çıkmaktadır.

2.2. Etkileşim Çizelgesi

Bu noktada etkileşim çizelgesini oluşturabiliriz. Bu amaçla: “Bu problemi yönetilebilir olacak biçimde ne kadar küçük parçalara bölebilirim?” sorusuna yanıt vermemiz gerekir.

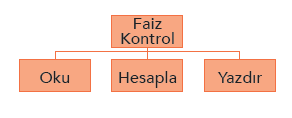
2.3. GSÇ Çizelgesi

2.4. Birleşim Çizelgesi ve Veri Sözlüğü

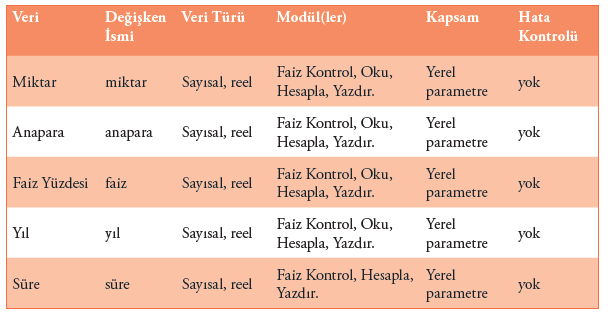
Birleşim çizelgesi hangi değişkenlerin bir modülden diğerine geçtiğini gösterir. Veri sözlüğü ise her bir modülün hangi değişkenleri kullandığını ve kapsamını belirtir. İlgili problem için birleşim çizelgesi aşağıda görülmektedir.

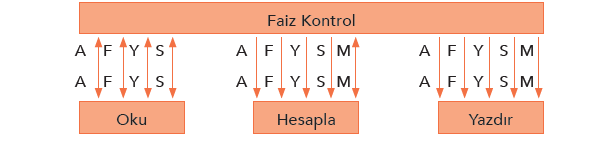
Yine ilgili problem için oluşturulan veri sözlüğü ise şu şekildedir:

2.5. Algoritma ve Akış Şemaları

Bu çizelgeleri oluşturduktan sonra artık algoritma ve akış şemalarını hazırlamaya geçebiliriz.

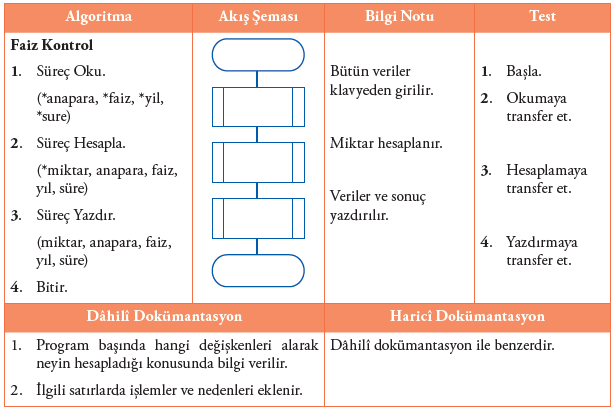
Faiz kontrolü modülü için gerekli algoritma ve akış şemasını hazırladıktan sonra sırası ile diğer modülleri oluşturalım. Oku modülüne bakalım.

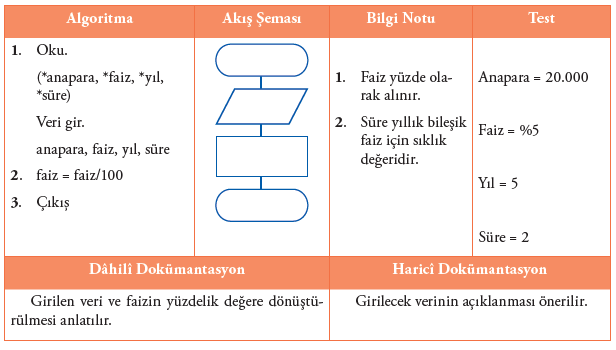
Şimdi ise hesapla modülü için ilgili işlemleri yapalım.

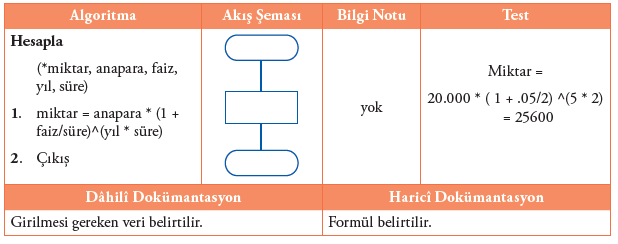
Son olarak yazdır modülüne göz atalım.

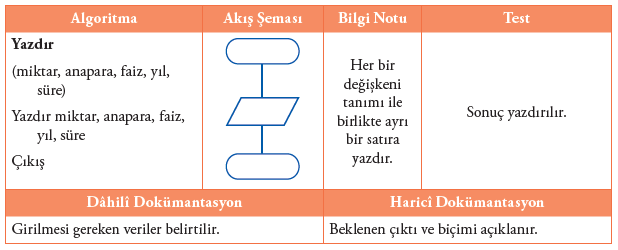
2.6. Çözümün Test Edilmesi:

Çözüm süreci sonucunda ortaya çıkan ürün, algoritma oluşturma programı yardımıyla çalıştırılarak her adımın doğru çalışıp çalışmadığı test edilmelidir. Hata tespiti durumunda sürecin ilgili basamakları gözden geçirilerek hatalar giderilip çözüme ulaşılmalıdır.

---

Doğrusal Mantık Yapısı İle Problem Çözme konusu ile ilgili sunum dosyasına ve konu testine (yakında) aşağıdan ulaşabilirsiniz.